에라토스테네스의 체 JS 소수 찾기 알고리즘 만들기

에라토스테네스의 체를 이용한 자바스크립트 소수 찾기 로직

소개: 에라토스테네스의 체란 무엇인가?

에라토스테네스의 체는 고대 그리스 수학자 에라토스테네스가 발명한 알고리즘으로, 특정 범위 내에서 소수를 찾는 가장 효율적인 방법 중 하나입니다. 이 방법은 특정 수의 배수를 제거해 나가며 소수만을 남기는 방식으로, 컴퓨터 과학에서도 널리 쓰이고 있습니다. 자바스크립트를 이용해 이 알고리즘을 구현한다면, 소수를 빠르고 효율적으로 찾을 수 있습니다.

자바스크립트로 에라토스테네스의 체 구현하기

자바스크립트를 사용하여 에라토스테네스의 체 알고리즘을 구현하는 과정은 다음과 같습니다:

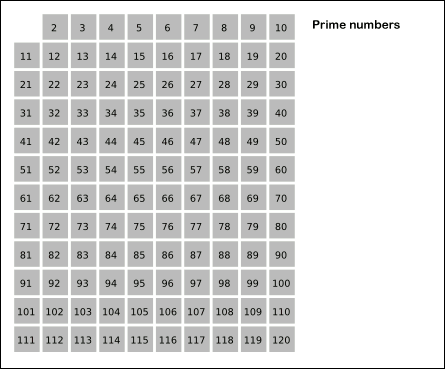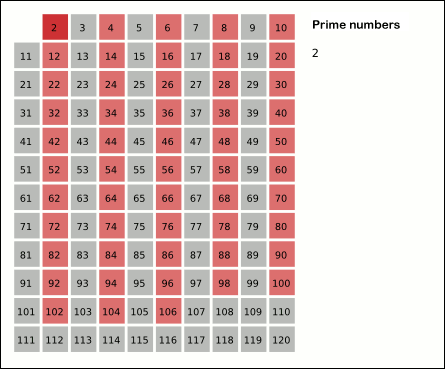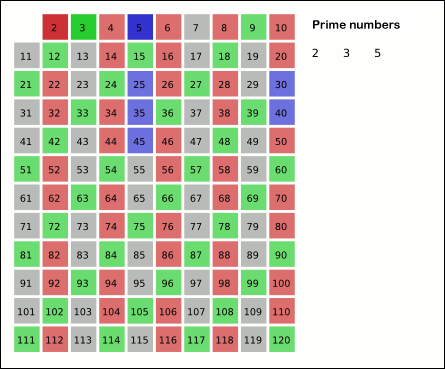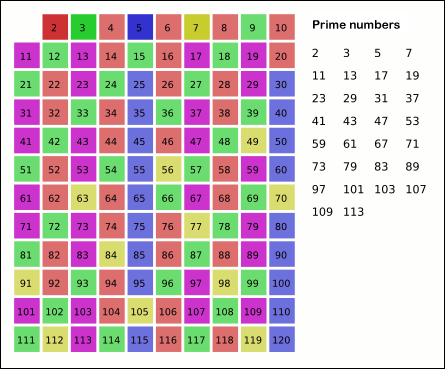
1. 초기화: 먼저, 소수를 찾고자 하는 범위까지의 모든 숫자를 포함하는 배열을 생성합니다. 이 배열은 초기에 모든 숫자가 소수라고 가정합니다.
2. 필터링: 가장 작은 소수인 2부터 시작하여, 해당 숫자의 배수들을 배열에서 제거합니다. 이 과정은 제곱근(√) 범위 내의 모든 숫자에 대해 반복됩니다.
3. 결과 반환: 남은 숫자들이 바로 해당 범위 내의 모든 소수입니다.

예제 코드

function findPrimes(max) {
    let sieve = [], i, j, primes = [];
    for (i = 2; i <= max; ++i) {
        if (!sieve[i]) {
            // i가 소수인 경우
            primes.push(i);
            for (j = i << 1; j <= max; j += i) {
                sieve[j] = true;
            }
        }
    }
    return primes;
}

console.log(findPrimes(100)); // 100까지의 소수 출력

자바스크립트에서 에라토스테네스의 체의 효율성

자바스크립트로 구현된 에라토스테네스의 체는 큰 수에 대해서도 빠르고 효율적으로 소수를 찾을 수 있습니다. 이 알고리즘의 시간 복잡도는 O(n log log n)으로, 매우 큰 범위의 숫자에 대해서도 빠르게 작동합니다. 또한, 메모리 사용 측면에서도 효율적이며, 복잡한 수학적 연산 없이 간단한 반복문과 배열을 이용해 구현할 수 있다는 장점이 있습니다.

에라토스테네스의 체를 자바스크립트로 구현하는 것은 프로그래밍 능력을 향상시키는 데에도 도움이 되며, 알고리즘의 이해도를 높이는 데에도 유용합니다. 효율적인 소수 찾기 로직을 필요로 하는 다양한 프로그래밍 문제나 프로젝트에 적용할 수 있어, 자바스크립트 개발자라면 반드시 익혀두어야 할 기술 중 하나입니다.

에라토스테네스의 체: 수학과 역사의 만남

에라토스테네스의 체란 무엇인가?

에라토스테네스의 체는 소수를 찾아내는 간단하면서도 효율적인 방법입니다. 이 방법은 기원전 3세기에 살았던 그리스의 수학자 에라토스테네스가 고안했습니다. 그의 이름을 따서 '에라토스테네스의 체(Sieve of Eratosthenes)'라고 불리우며, 소수를 찾는 고전적인 방법 중 하나로 꼽힙니다.

소수란 무엇인가?

소수는 1과 자기 자신으로만 나누어 떨어지는 1보다 큰 자연수를 말합니다. 예를 들어, 2, 3, 5, 7 등은 소수입니다. 소수는 수학의 여러 분야에서 중요한 역할을 합니다.

에라토스테네스의 체의 작동 원리

에라토스테네스의 체는 다음과 같은 단계로 소수를 찾습니다:

1. 2부터 시작하여, 특정 범위 내의 모든 자연수를 나열합니다.
2. 가장 작은 수인 2를 소수로 선택하고, 2의 배수를 모두 지웁니다.
3. 다음으로 작은 수를 소수로 선택하고, 그 배수를 모두 지웁니다.
4. 이 과정을 반복하여, 남은 수들이 모두 소수가 될 때까지 계속합니다.

수학적 의미와 중요성

이 방법은 매우 단순하지만, 소수를 찾는 데 있어서 매우 효율적입니다. 에라토스테네스의 체는 소수에 대한 이해를 돕고, 소수의 패턴을 발견하는 데 도움을 줍니다. 또한 컴퓨터 과학에서 알고리즘의 기본적인 개념을 이해하는 데에도 중요한 역할을 합니다.

현대적 응용

현대에 와서 에라토스테네스의 체는 컴퓨터 알고리즘에서 중요한 위치를 차지합니다. 특히 암호학에서 소수의 중요성이 높아지면서, 이 방법은 소수를 찾기 위한 알고리즘으로 널리 사용되고 있습니다.

에라토스테네스의 체는 수학의 역사에서 중요한 발견 중 하나로, 오늘날에도 그 가치가 인정받고 있습니다. 이 방법은 소수를 찾는 기본적이면서도 중요한 도구로, 수학과 컴퓨터 과학을 공부하는 데 있어 필수적인 지식입니다.